An aspherical lens is any lens with an optical surface that is not spherical, incorporating cylindrical, toroidal, and general freeform surfaces. In precision optics, the term “asphere” typically refers to a lens where the local radius of curvature changes from the center of the optical axis to the edge, and is rotationally symmetrical about the optical axis. As shown in the equation below, the general asphere equation allows for the precise definition of these surfaces. The terms ( z ), ( x ), ( k ), ( R ), and ( A_n ) are key to understanding aspheres.
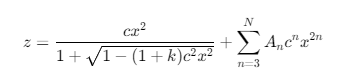
( z ): The surface sag, the height difference from the vertex of the surface to a point on the surface.
( x ): The distance from the center of the lens along the optical axis.
( k ): The conic constant, which defines the shape of the conic section.
( R ): The base radius, the radius at the center of the lens.
( A_n ): Polynomial expansion terms to describe the aspheric shape more accurately. The ability of aspherics to correct aberrations more effectively than spherical lenses makes them crucial in high-performance optical systems. This allows for a more compact and lighter optical train by reducing the number of components required and improving the overall system performance.
Using aspherics incurs a cost trade-off compared to traditional spherical lenses, as they are more expensive to manufacture due to the specialized knowledge and technologies required. However, the benefits outweigh the costs in many applications. Key advantages include:
Reduced Aberrations: Aspheres can correct various aberrations such as spherical aberration, coma, and astigmatism more efficiently.
Smaller Optical Systems: Using aspherics can reduce the overall size and weight of optical systems by minimizing the number of lens elements needed.
Higher Performance: Enhances the optical system's performance by allowing more precise control over wavefront distortion.
In the example below, a spherical lens on the left fails to focus a collimated beam of light accurately, creating a large spot size and reducing the power density of a laser. In contrast, the aspheric lens on the right focuses the light evenly, improving the power density dramatically.
The image below demonstrates the impact of adding an aspheric lens in an optical system. By incorporating an asphere, the system maintains excellent performance, reducing the number of elements and creating a more compact design. !
Aspheric lenses pose significant manufacturing challenges due to their ever-changing local radius curvature. Traditional spherical tools and techniques are not suitable for grinding, polishing, and measuring these surfaces. Modern production tools include single-point or sub-aperture grinding and polishing methods, which process only a small portion of the lens at a time. This increases processing time and limits the number of lenses that can be ground or polished simultaneously. Depending on the specific requirements, aspheric lenses can be molded or diamond turned. Molded aspheres are particularly useful for high-volume production, while diamond turning is more versatile but time-consuming.
Profilometers are essential metrology tools for aspherics, measuring a single point at a time while scanning the surface. The basic profilometer measurement involves a single trace from one edge to the other, through the vertex. More advanced profilometers can perform raster or spiral scans to provide a full map of surface errors.
| Profiling Method | Description |
| Single Trace | Measures a single path from edge to edge, through vertex. |
| RasterScan | Maps the entire surface using a grid of points. |
| SpiralScan | Scans the surface in a spiral pattern to cover more area. |
| Some profilometers may contact the surface with a stylus, while others use non-contact methods. Non-contact methods are generally preferred to avoid surface damage. | |
Forbes polynomials, ( Q_{\text{con}} ) and ( Q_{\text{bfs}} ), are alternative representations to the traditional asphere equation. These polynomials have characteristics that facilitate design for manufacturability. Not all processing and metrology tools support these equations, so it's important to choose tools that are compatible.
Aspheric lenses can have inflection points where the local radius changes sign, from convex to concave, which can increase manufacturing and measurement complexity. Gullwings are extreme cases of aspheres with inflection points where the sag turns back on itself, further complicating the manufacturing process.
Asphere:
Base Radius (R): The radius used in the aspheric definition. This is the same as the vertex radius unless an ( A_2 ) term is used (strongly discouraged).
Local Radius: Radius of curvature at a given location on the asphere. Unlike a spherical surface, the local radius is constantly changing on an asphere.
Vertex Radius: The local radius of curvature on the rotational axis (center) of the asphere.
Best Fit Sphere (BFS): The radius of the sphere which intersects both the vertex and the edge of the aspheric surface over a given aperture. It is aperture-dependent.
Sag: The height difference from the vertex of the asphere to a point in question.
Departure: Difference between the theoretical sag of the aspheric surface and the BFS.
Conic Constant (k): Defines the section of a conic to use as the base of the asphere.
Understanding and leveraging aspheric lenses is essential for designing and manufacturing high-performance optical systems. While they present unique challenges in terms of manufacturing and metrology, their benefits in correcting aberrations and achieving high performance make them indispensable in modern optical engineering. If you need custom precision optics with aspherics, CNGeir can help. Our advanced manufacturing processes and metrology tools ensure the highest quality aspheric lenses. Contact us to discuss your project requirements and let us help you achieve the best optical performance for your applications.
 Call us on:
Call us on:  Email Us:
Email Us:  No.9 Zhongxing East Road, Lishui Economic Development Zone, Nanjing, Jiangsu, China
No.9 Zhongxing East Road, Lishui Economic Development Zone, Nanjing, Jiangsu, China